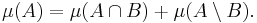Borel regular measure

In mathematics, an outer measure μ on n-dimensional Euclidean space Rⁿ is called Borel regular if the following two conditions hold:

• Every Borel set B ⊆ Rⁿ is μ-measurable in the sense of Carathéodory's criterion: for every A ⊆ Rⁿ,

• For every set A ⊆ Rⁿ (which need not be μ-measurable) there exists a Borel set B ⊆ Rⁿ such that A ⊆ B and μ(A) = μ(B).

An outer measure satisfying only the first of these two requirements is called a Borel measure, while an outer measure satisfying only the second requirement is called a regular measure.

The Lebesgue outer measure on Rⁿ is an example of a Borel regular measure.

It can be proved that a Borel Regular measure, although introduced here as an outer measure (only countably subadditive), becomes a full measure (countably additive) if restricted to the Borel sets.

References

• Evans, Lawrence C.; Gariepy, Ronald F. (1992). Measure theory and fine properties of functions. CRC Press. ISBN 0849371570. 

• Taylor, Angus E. (1985). General theory of functions and integration. Dover Publications. ISBN 0486649881. 

• Fonseca, Irene; Gangbo, Wilfrid (1995). Degree theory in analysis and applications. Oxford University Press. ISBN 0198511965.